Discrete-Event Simulation concerns the modeling of a stochastic system as it evolves over time, events occur at distinct points of time, which change the state variables, nothing happens between two consecutive events. Consider a single-server queueing system: Customers arrive from a population into a system and either go into service immediately (if the server is not busy) or join a waiting line.
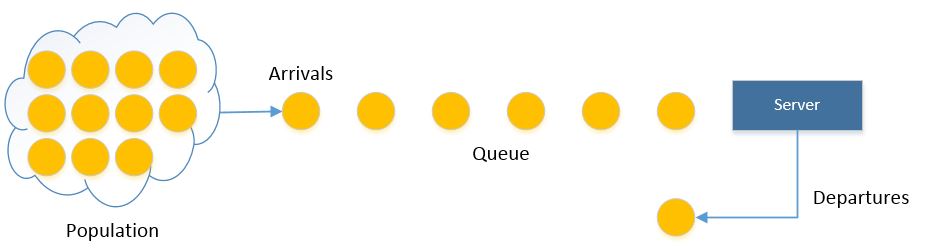
In a simulation, this system begins empty and the first arrival (first event) takes place at clock time 0. The first arrival finds the server available (or idle) and gets served immediately and for a certain period of time, the next arrivals can find the server busy, in that case, the customer joins the waiting line. The following distributions can be used in order to generate interarrival and service times:
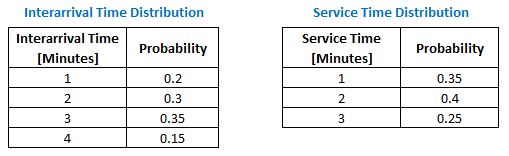
Note that the sum of probabilities must equal 1 in all cases. Through these time distributions events will be generated. In other words, arrivals into the system and departures from the system will be scheduled to take place at certain points in time, this information is registered in the Event List. Time in a simulation is maintained using the already mentioned clock-time variable which is also included in the event list.
