Simulation is basically a technique used for analyzing systems with a certain level of complexity, real-world problems can technically be represented as stochastic/mathematical models. In doing so, however, the conditions of such problems might be severely simplified, causing that the solutions are likely to be inferior or inadequate for implementation. That’s why Simulation is often the only reasonable alternative for modeling the real-world.
| Advantages | Disadvantages |
|---|---|
| Straightforward implementation | Not an optimization technique |
| Great flexibility | Can be costly |
Contrary to the mathematical solutions, a simulation involves running a model through time (normally on a computer) to generate realistic results, this means that simulation imitates the operation of a real-world system as it evolves over time. The main goal of a simulation study is cleary to simulate a system, but we can’t simulate a system without understanding what it is. Schmidt and Taylor proposed in 1970 probably the best definition of a system:
A system is defined to be a collection of entities, e.g. people or machines, that act and interact together toward the accomplishment of some logical end.
This definition is flexible, a system can also be composed of many subsystems, it all depends on the particular case study, what may be a system for a study may be only a subsystem for another and so on. In a simulation study, systems tend to be dynamic because they change their status over time. The concept of state of a system is used to describe this status:
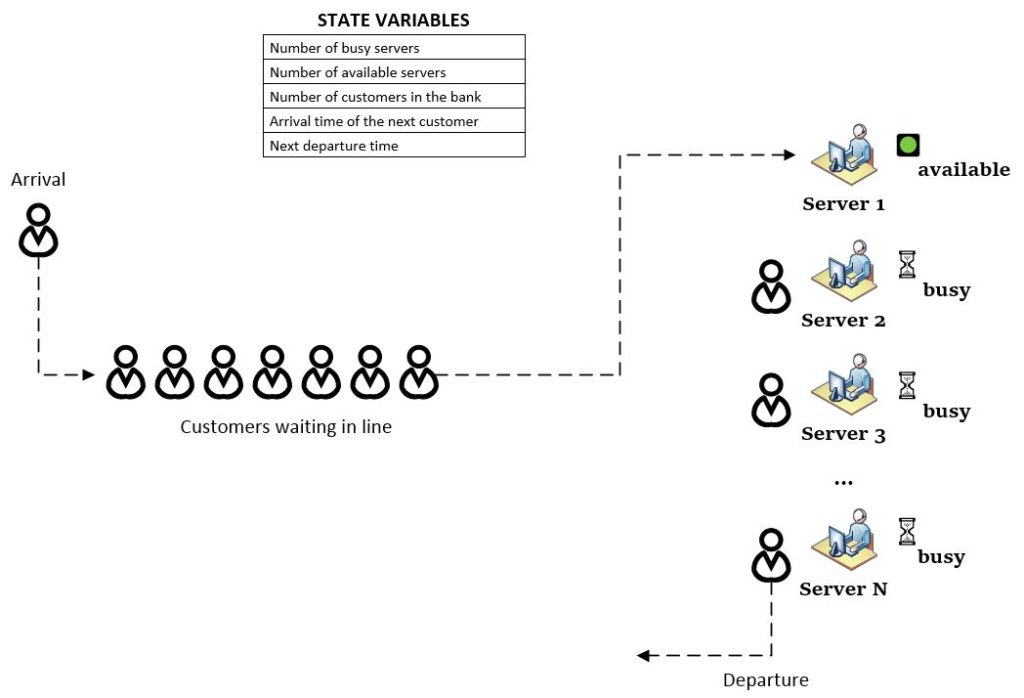
The state of a system is the collection of variables necessary to describe the status of the system at any given time, as an example of a system, let us consider a bank. This system consists of the servers and the customers waiting in line to be served, as customers arrive or depart, the status of the system changes:
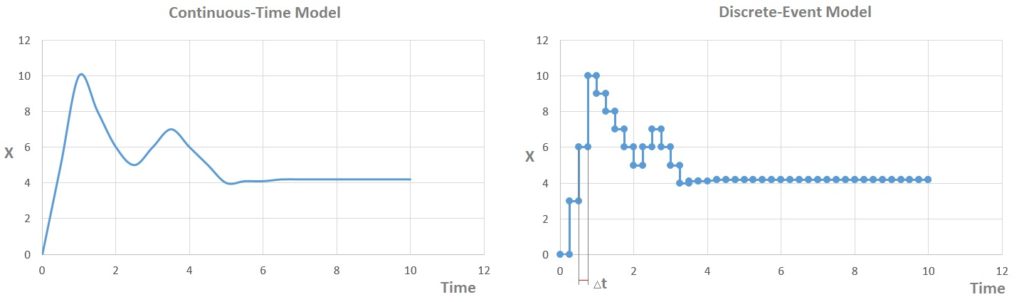
Systems may be classified as discrete or continuous:
A discrete system is one in which the state variables are countable and they change at discrete points in time. Because of the fact that these systems have a countable number of states, they can be modeled using precise mathematical expressions.
(Example) A bank or any facility in which a service is done is an example of a discrete system since the state variables change only when an entity arrives to get served, or when this entity departs after being served. These changes take place at discrete points in time.
A continuous system is one in which the state variables change continuously over time. These systems are usually modeled by sets of either ordinary or partial differential equations possibly coupled with algebraic equations.
(Example) A reaction vessel in which a chemical process takes place is an example of a continuous system since the amounts of substances change continuously over time.
Our example of a bank is a continuous system
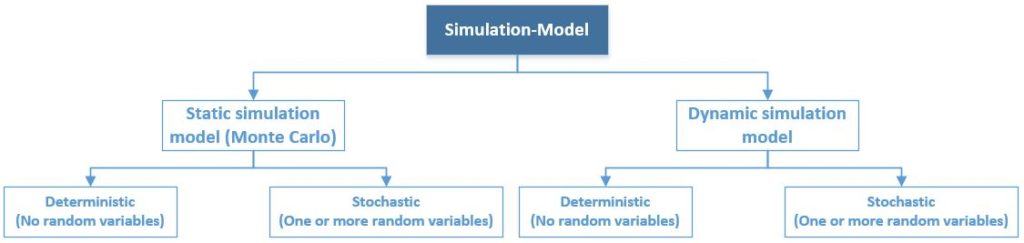
Simulation models
In a strict sense, there are two types of simulation models: